CAGR berechnen

Der CAGR (compound annual growth rate) oder die durchschnittliche jährliche Wachstumsrate lässt sich mit einer Formel oder auch mit der ZSATZINVEST-Funktion berechnen. Dabei kann man mit dem CAGR nicht Jahre, sondern auch andere Zeiträume wie z.B. Monate oder Tage betrachten. Allgemein geht es nur darum, die durchschnittliche Wachstumsrate in einem Zeitraum, der aus mehreren Perioden besteht, zu ermitteln. Mit dem CAGR kann man Fragen wie z.B. "Wie stark ist die Bevölkerung in Deutschland in den letzten 10 Jahre im Schnitt pro Jahr gewachsen?" beantworten.

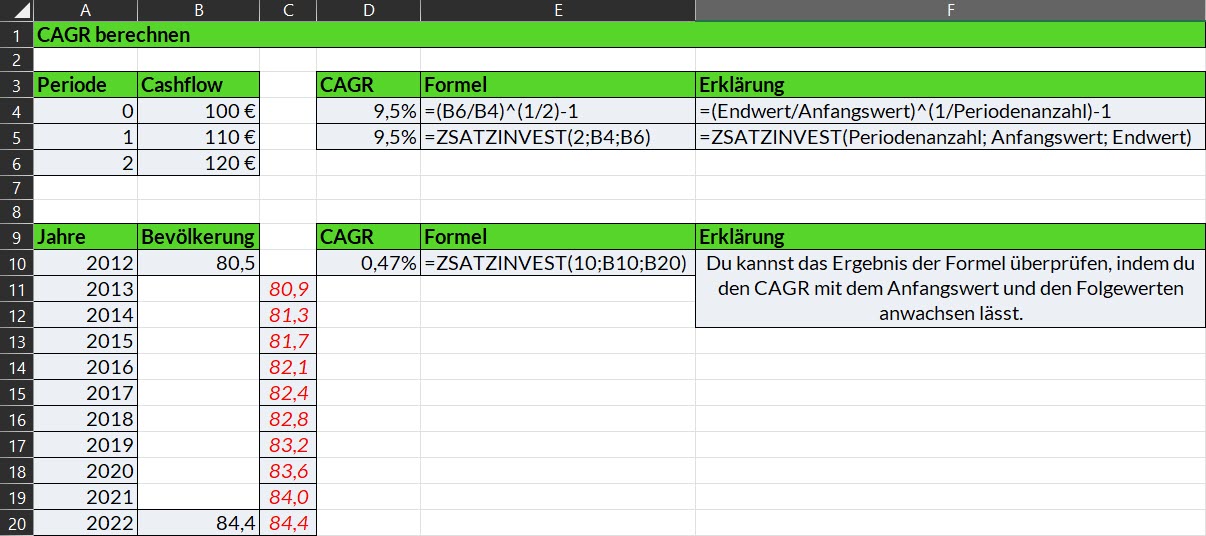
CAGR mit Formel berechnen

Um den CAGR mit einer Formel zu berechnen, musst Du den Endwert hier 120 € durch 100 € teilen und dann hoch 1 durch Periodenanzahl nehmen und am Ende 1 abziehen. ^(1/Periodenanzahl) ist das gleiche wie die x-te Wurzel ziehen. Wenn es sich z.B. um 2 Perioden handelt, ist ^(1/2) das gleiche, wie als würden wir die Wurzel ziehen. Bei 3 Perioden ^(1/3) wäre dies die 3. Wurzel usw.  

Wichtig ist, dass es sich bei der Periodenanzahl um die Anzahl der Wachstumsphasen handelt. In dem ersten Beispiel sind dies 2, also von 100 auf 110 und von 110 auf 120. Also die Anzahl der Zeilen minus 1.

Beim zweiten Beispiel mit der Bevölkerungszahl sind dies 10 Perioden (2022-2012) bzw. 11 minus 1 Zeilen.

CAGR mit ZSATZINVEST-Funktion berechnen

Um den CAGR zu berechnen, können wir auch die ZSATZINVEST-Funktion verwenden.

Zzr = Anzahl der Perioden für die Investition - Periodenanzahl
Bw = Der aktuelle Wert der Investition (Barwert) - Anfangswert
Zw= Der zukünftige Wert der Investition (Zukunftswert) - Endwert

Mit der Funktion wird das Ganze schon übersichtlicher. Wichtig ist hier auch wieder, dass man die korrekte Anzahl der Perioden eingibt. Wenn Du Dir nicht sicher bist, kannst Du auch den errechneten CAGR nehmen und diesen verwenden, um den Anfangswert um die Anzahl der Perioden anwachsen zu lassen. Somit lässt sich prüfen, ob man mit der durchschnittlichen Wachstumsrate auf den richtigen Endwert kommt.